



Next: Algunas herramientas de
seguridad Up: Otros aspectos de la Previous: Otros aspectos de la Índice
General
Subsecciones
En el mundo real, si una universidad quiere proteger los expedientes de
sus alumnos los guardará en un armario ignífugo, bajo llave y vigilado
por guardias, para que sólo las personas autorizadas puedan acceder a ellos
para leerlos o para modificarlos; si queremos proteger nuestra correspondencia
de curiosos, simplemente usamos un sobre; si no queremos que nos roben dinero,
lo guardamos en una caja fuerte... Lamentablemente, en una red no disponemos de
todas estas medidas que nos parecen habituales; la principal (podríamos
decir única) forma de protección va a venir de la mano de
la criptografía. El cifrado de los datos nos va a permitir desde proteger
nuestro correo personal para que ningún curioso lo pueda leer, hasta controlar
el acceso a nuestros archivos de forma que sólo personas autorizadas puedan
examinar (o lo que quizás es más importante, modificar) su contenido,
pasando por proteger nuestras claves cuando conectamos a un sistema remoto o nuestros
datos bancarios cuando realizamos una compra a través de Internet. Hemos
presentado con anterioridad algunas aplicaciones que utilizan de una u otra forma
la criptografía para proteger nuestra información; aquí intentaremos
dar unas bases teóricas mínimas sobre términos, algoritmos,
funciones...utilizadas en ese tipo de aplicaciones. Para más referencias
es imprescindible la obra [Sch94]; otras publicaciones interesantes son [MvOV96],
[Den83], [Sal90] y, para temas de criptoanálisis, [otUAH90]. Un texto básico para aquellos que no
disponen de mucho tiempo o que sólo necesitan una perspectiva general de
la criptografía puede ser [Cab96].
La criptología (del griego krypto y logos, estudio
de lo oculto, lo escondido) es la ciencia15.1 que trata los problemas
teóricos relacionados con la seguridad en el intercambio de mensajes en
clave entre un emisor y un receptor a través de un canal de comunicaciones
(en términos informáticos, ese canal suele ser una red de computadoras).
Esta ciencia está dividida en dos grandes ramas: la criptografía,
ocupada del cifrado de mensajes en clave y del diseño de criptosistemas
(hablaremos de éstos más adelante), y el criptoanálisis,
que trata de descifrar los mensajes en clave, rompiendo así el criptosistema.
En lo sucesivo nos centraremos más en la criptografía y los criptosistemas
que en el criptoanálisis, ya que nos interesa, más que romper sistemas
de cifrado (lo cual es bastante complicado cuando trabajamos con criptosistemas
serios), el saber cómo funcionan éstos y conocer el diseño
elemental de algunos sistemas seguros.
La criptografía es una de las ciencias consideradas como más antiguas,
ya que sus orígenes se remontan al nacimiento de nuestra civilización.
Su uso original era el proteger la confidencialidad de informaciones militares
y políticas, pero en la actualidad es una ciencia interesante no sólo
en esos círculos cerrados, sino para cualquiera que esté interesado
en la confidencialidad de unos determinados datos: actualmente existe multitud
de software y hardware destinado a analizar y monitorizar el tráfico de
datos en redes de computadoras; si bien estas herramientas constituyen un avance
en técnicas de seguridad y protección, su uso indebido es al mismo
tiempo un grave problema y una enorme fuente de ataques a la intimidad de los
usuarios y a la integridad de los propios sistemas. Aunque el objetivo original
de la criptografía era mantener en secreto un mensaje, en la actualidad
no se persigue únicamente la privacidad o confidencialidad de los
datos, sino que se busca además garantizar la autenticación
de los mismos (el emisor del mensaje es quien dice ser, y no otro), su integridad
(el mensaje que leemos es el mismo que nos enviaron) y su no repudio (el
emisor no puede negar el haber enviado el mensaje).
Podemos dividir la historia de la criptografía en tres periodos fundamentales;
hasta mediados de siglo, tenemos la criptología precientífica, considerada
no una ciencia sino más bien un arte. En 1949, Shannon logró cimentar
la criptografía sobre unas bases matemáticas ([Sha49]),
comenzando el período de la criptografía científica. Menos
de treinta años después, en 1976, Diffie y Hellman publicaron sus
trabajos sobre criptografía de clave pública ([DH76]), dando lugar al período de criptografía
de clave pública, que dura hasta la actualidad.
Matemáticamente, podemos definir un criptosistema como una cuaterna de
elementos { }, formada por:
}, formada por:
- Un conjunto finito llamado alfabeto,
 , a partir del cual, y utilizando ciertas normas sintácticas
y semánticas, podremos emitir un mensaje en claro ( plain text
) u obtener el texto en claro correspondiente a un mensaje cifrado ( cipher
text). Frecuentemente, este alfabeto es el conjunto de los enteros módulo
q,
, a partir del cual, y utilizando ciertas normas sintácticas
y semánticas, podremos emitir un mensaje en claro ( plain text
) u obtener el texto en claro correspondiente a un mensaje cifrado ( cipher
text). Frecuentemente, este alfabeto es el conjunto de los enteros módulo
q,  , para un
, para un  dado.
dado.
- Otro conjunto finito denominado espacio de claves,
 , formado por todas las posibles claves, tanto de cifrado
como de descifrado, del criptosistema.
, formado por todas las posibles claves, tanto de cifrado
como de descifrado, del criptosistema.
- Una familia de aplicaciones del alfabeto en sí mismo,
 , llamadas transformaciones de cifrado.
El proceso de cifrado se suele representar como
, llamadas transformaciones de cifrado.
El proceso de cifrado se suele representar como

(k,a)=c,
 ,
,  y
y  .
.
- Otra familia de aplicaciones del alfabeto en sí mismo,
 , llamadas transformaciones de descifrado.
Análogamente al proceso de cifrado, el de descifrado se representa
como
, llamadas transformaciones de descifrado.
Análogamente al proceso de cifrado, el de descifrado se representa
como
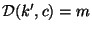
,
 ,
,  y
y  .
.
Muchos autores dividen a su vez un miembro de esta cuaterna, el alfabeto, en dos
espacios diferentes: el espacio de mensajes,  , formado por los textos en claro que se pueden formar
con el alfabeto, y el espacio de cifrados,
, formado por los textos en claro que se pueden formar
con el alfabeto, y el espacio de cifrados,  , formado por todos los posibles criptogramas que el cifrador es
capaz de producir. Sin embargo, tanto el texto en claro como el cifrado han de
pertenecer al alfabeto, por lo que hemos preferido no hacer distinciones entre
uno y otro, agrupándolos en el conjunto
, formado por todos los posibles criptogramas que el cifrador es
capaz de producir. Sin embargo, tanto el texto en claro como el cifrado han de
pertenecer al alfabeto, por lo que hemos preferido no hacer distinciones entre
uno y otro, agrupándolos en el conjunto  para simplificar los
conceptos que presentamos. Así, un criptosistema presenta la estructura
mostrada en la figura 14.1.
para simplificar los
conceptos que presentamos. Así, un criptosistema presenta la estructura
mostrada en la figura 14.1.
 Figura 14.1: Estructura de un criptosistema
Figura 14.1: Estructura de un criptosistema
El emisor emite un texto en claro, que es tratado por un cifrador con la ayuda
de una cierta clave, k, creando un texto cifrado (criptograma). Este criptograma
llega al descifrador a través de un canal de comunicaciones (como hemos
dicho antes, para nosotros este canal será habitualmente algún tipo
de red). El descifrador convierte el criptograma de nuevo en texto claro, apoyándose
ahora en otra clave, k´ (veremos más adelante que esta clave puede
o no ser la misma que la utilizada para cifrar), y este texto claro ha de coincidir
con el emitido inicialmente para que se cumplan los principios básicos
de la criptografía moderna. En este hecho radica toda la importancia de
los criptosistemas.
Es obvio, a la vista de lo expuesto anteriormente, que el elemento más
importante de todo el criptosistema es el cifrador, que ha de utilizar el algoritmo
de cifrado para convertir el texto claro en un criptograma. Usualmente, para hacer
esto, el cifrador depende de un parámetro exterior, llamado clave de
cifrado (o de descifrado, si hablamos del descifrador) que es aplicado a una
función matemática irreversible (al menos, computacionalmente):
no es posible invertir la función a no ser que se disponga de la clave
de descifrado. De esta forma, cualquier conocedor de la clave (y, por supuesto,
de la función), será capaz de descifrar el criptograma, y nadie
que no conozca dicha clave puede ser capaz del descifrado, aún en el caso
de que se conozca la función utilizada.
La gran clasificación de los criptosistemas se hace en función de
la disponibilidad de la clave de cifrado/descifrado. Existen, por tanto, dos grandes
grupos de criptosistemas:
Denominamos criptosistema de clave secreta (de clave privada, de clave única
o simétrico) a aquel criptosistema en el que la clave de cifrado,  , puede ser calculada a partir
de la de descifrado,
, puede ser calculada a partir
de la de descifrado,  , y viceversa. En la mayoría de estos
sistemas, ambas claves coinciden, y por supuesto han de mantenerse como un secreto
entre emisor y receptor: si un atacante descubre la clave utilizada en la comunicación,
ha roto el criptosistema.
, y viceversa. En la mayoría de estos
sistemas, ambas claves coinciden, y por supuesto han de mantenerse como un secreto
entre emisor y receptor: si un atacante descubre la clave utilizada en la comunicación,
ha roto el criptosistema.
Hasta la década de los setenta, la invulnerabilidad de todos los sistemas
dependía de este mantenimiento en secreto de la clave de cifrado. Este
hecho presentaba una gran desventaja: había que enviar, aparte del criptograma,
la clave de cifrado del emisor al receptor, para que éste fuera capaz de
descifrar el mensaje. Por tanto, se incurría en los mismos peligros al
enviar la clave, por un sistema que había de ser supuestamente seguro,
que al enviar el texto plano. De todos los sistemas de clave secreta, el único
que se utiliza en la actualidad es DES ( Data Encryption Standard, que
veremos más adelante). Otros algoritmos de clave privada, como el cifrado
Caesar o el criptosistema de Vigenère (serán también brevemente
comentados más adelante) han sido criptoanalizados con éxito, lo
cual da una idea del porqué del desuso en que han caído estos sistemas
(con la excepción de DES, que es seguramente el algoritmo de cifra más
utilizado en la actualidad). Por si esto no fuera suficiente, el hecho de que
exista al menos una clave de cifrado/descifrado entre cada dos usuarios de un
sistema haría inviable la existencia de criptosistemas simétricos
en las grandes redes de computadores de hoy en día: para un sistema de
computación con N usuarios, se precisarían  claves diferentes, lo cual es obviamente
imposible en grandes sistemas. Todos estos motivos han propiciado que el estudio
de los cifradores simétricos (excepto DES) quede relegado a un papel histórico.
claves diferentes, lo cual es obviamente
imposible en grandes sistemas. Todos estos motivos han propiciado que el estudio
de los cifradores simétricos (excepto DES) quede relegado a un papel histórico.
Los sistemas de cifrado de clave única se dividen a su vez en dos grandes
grupos de criptosistemas: por una parte tenemos los cifradores de flujo,
que son aquellos que pueden cifrar un sólo bit de texto claro al mismo
tiempo, y por tanto su cifrado se produce bit a bit, y por otro lado tenemos los
cifradores de bloque, que cifran un bloque de bits (habitualmente, cada
bloque es de 64 bits) como una única unidad.
En 1976, Whitfield Diffie y Martin Hellman, de la Universidad de Stanford, demostraron
la posibilidad de construir criptosistemas que no precisaran de la transferencia
de una clave secreta en su trabajo [DH76]. Esto
motivó multitud de investigaciones y discusiones sobre la criptografía
de clave pública y su impacto, hasta el punto que la NSA ( National
Security Agency ) estadounidense trató de controlar el desarrollo de
la criptografía, ya que la consideraban una amenaza peligrosa para la seguridad
nacional. Esta polémica ha llegado incluso hasta nuestros días,
en los que el affaire Zimmermann (el autor de PGP) o el Clipper Chip
han llenado portadas de periódicos de todo el mundo.
Veamos ahora en que se basan los criptosistemas de clave pública. En éstos,
la clave de cifrado se hace de conocimiento general (se le llama clave pública).
Sin embargo, no ocurre lo mismo con la clave de descifrado ( clave privada),
que se ha de mantener en secreto. Ambas claves no son independientes, pero del
conocimiento de la pública no es posible deducir la privada sin ningún
otro dato (recordemos que en los sistemas de clave privada sucedía lo contrario).
Tenemos pues un par clave pública-clave privada; la existencia de ambas
claves diferentes, para cifrar o descifrar, hace que también se conozca
a estos criptosistemas como asimétricos.
Cuando un receptor desea recibir una información cifrada, ha de hacer llegar
a todos los potenciales emisores su clave pública, para que estos cifren
los mensajes con dicha clave. De este modo, el único que podrá descifrar
el mensaje será el legítimo receptor, mediante su clave privada.
Matemáticamente, si  es el algoritmo
cifrador y
es el algoritmo
cifrador y  el descifrador, se ha de cumplir
que
el descifrador, se ha de cumplir
que

,
 un mensaje, y siendo
un mensaje, y siendo  y
y  las claves de descifrado y cifrado, respectivamente.
El criptoanálisis es la ciencia opuesta a la criptografía (quizás
no es muy afortunado hablar de ciencias opuestas, sino más bien
de ciencias complementarias), ya que si ésta trata principalmente
de crear y analizar criptosistemas seguros, la primera intenta romper esos sistemas,
demostrando su vulnerabilidad; es decir, trata de descifrar los criptogramas.
El término descifrar siempre va acompañado de discusiones
de carácter técnico, aunque asumiremos que descifrar es conseguir
el texto en claro a partir de un criptograma, sin entrar en polémicas de
reversibilidad y solidez de criptosistemas.
las claves de descifrado y cifrado, respectivamente.
El criptoanálisis es la ciencia opuesta a la criptografía (quizás
no es muy afortunado hablar de ciencias opuestas, sino más bien
de ciencias complementarias), ya que si ésta trata principalmente
de crear y analizar criptosistemas seguros, la primera intenta romper esos sistemas,
demostrando su vulnerabilidad; es decir, trata de descifrar los criptogramas.
El término descifrar siempre va acompañado de discusiones
de carácter técnico, aunque asumiremos que descifrar es conseguir
el texto en claro a partir de un criptograma, sin entrar en polémicas de
reversibilidad y solidez de criptosistemas.
En el análisis para establecer las posibles debilidades de un sistema de
cifrado, se han de asumir las denominadas condiciones del peor caso: (1) el criptoanalista
tiene acceso completo al algoritmo de encriptación, (2) el criptoanalista
tiene una cantidad considerable de texto cifrado, y (3) el criptoanalista conoce
el texto en claro de parte de ese texto cifrado. También se asume generalmente
el Principio de Kerckhoffs, que establece que la seguridad del cifrado
ha de residir exclusivamente en el secreto de la clave, y no en el mecanismo de
cifrado.
Aunque para validar la robustez de un criptosistema normalmente se suponen todas
las condiciones del peor caso, existen ataques más específicos,
en los que no se cumplen todas estas condiciones. Cuando el método de ataque
consiste simplemente en probar todas y cada una de las posibles claves del espacio
de claves hasta encontrar la correcta, nos encontramos ante un ataque de fuerza
bruta o ataque exhaustivo. Si el atacante conoce el algoritmo de cifrado
y sólo tiene acceso al criptograma, se plantea un ataque sólo
al criptograma. Un caso más favorable para el criptoanalista se produce
cuando el ataque cumple todas las condiciones del peor caso; en este caso, el
criptoanálisis se denomina de texto en claro conocido. Si además
el atacante puede cifrar una cantidad indeterminada de texto en claro al ataque
se le denomina de texto en claro escogido; este es el caso habitual de
los ataques contra el sistema de verificación de usuarios utilizado por
Unix, donde un intruso consigue la tabla de contraseñas (generalmente
/etc/passwd) y se limita a realizar cifrados de textos en claro de su elección
y a comparar los resultados con las claves cifradas (a este ataque también
se le llama de diccionario, debido a que el atacante suele utilizar un
fichero 'diccionario' con los textos en claro que va a utilizar). El caso más
favorable para un analista se produce cuando puede obtener el texto en claro correspondiente
a criptogramas de su elección; en este caso el ataque se denomina de
texto cifrado escogido. Por último, si el atacante simplemente se limita
a probar todas y cada una de las posibles contraseñas, estamos ante un
ataque de fuerza bruta.
Cualquier algoritmo de cifrado, para ser considerado seguro, ha de soportar todos
estos ataques y otros no citados; sin embargo, en la criptografía, como
en cualquier aspecto de la seguridad, informática o no, no debemos olvidar
un factor muy importante: las personas. El sistema más robusto caerá
fácilmente si se tortura al emisor o al receptor hasta que desvelen el
contenido del mensaje, o si se le ofrece a uno de ellos una gran cantidad de dinero;
este tipo de ataques (sobornos, amenazas, extorsión, tortura...) se consideran
siempre los más efectivos.
El cifrado Caesar (o César) es uno de los más antiguos que se conocen.
Debe su nombre al emperador Julio César, que presuntamente lo utilizó
para establecer comunicaciones seguras con sus generales durante las Guerras Gálicas.
Matemáticamente, para trabajar con el cifrado Caesar, tomamos el alfabeto
 (enteros de módulo m). Cuando
(enteros de módulo m). Cuando
 y
y  son primos entre
sí, la aplicación
son primos entre
sí, la aplicación  ,
,  , recibe el nombre de codificación
módulo m con parámetros a, b; el par
, recibe el nombre de codificación
módulo m con parámetros a, b; el par  es la clave de este criptosistema.
es la clave de este criptosistema.
Así, trabajando con el alfabeto inglés (para nosotros resulta conveniente
tomar este alfabeto, de uso más extendido en Informática que el
español; la única diferencia radica en el uso de la letra ñ),
podemos tomar el alfabeto definido por  . Asignamos a cada letra (a..z) un entero módulo 26,
de la siguiente forma:
. Asignamos a cada letra (a..z) un entero módulo 26,
de la siguiente forma:
| A=0 |
B=1 |
C=2 |
D=3 |
E=4 |
F=5 |
| G=6 |
H=7 |
I=8 |
J=9 |
K=10 |
L=11 |
| M=12 |
N=13 |
O=14 |
P=15 |
Q=16 |
R=17 |
| S=18 |
T=19 |
U=20 |
V=21 |
W=22 |
X=23 |
| Y=24 |
Z=25 |
|
|
|
|
El cifrado Caesar siempre utiliza la clave (1,b), es decir, siempre tomaremos
a=1. De esta forma, la anterior aplicación quedará f(x)=x+b, lo
cual se traduce sencillamente en que para encriptar una letra hemos de tomar su
entero correspondiente y sumarle b (la clave del criptosistema) para obtener el
texto cifrado. Análogamente, y gracias al hecho que f(x) siempre ha de
ser biyectiva, independientemente del valor de b, para descifrar un texto tomamos
la función inversa, definida por f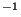 (x)=x-b. Veamos un sencillo ejemplo,
en el que se toma b=4: Queremos cifrar, con la clave (1,4), la palabra CESAR
. Tomando el valor de cada letra, tenemos el equivalente numérico de la
palabra:
Aplicamos a cada número la función f(x)=x+4 para obtener
que retornado al alfabeto inglés, sustituyendo cada valor por su equivalente,
queda GIWEV .
(x)=x-b. Veamos un sencillo ejemplo,
en el que se toma b=4: Queremos cifrar, con la clave (1,4), la palabra CESAR
. Tomando el valor de cada letra, tenemos el equivalente numérico de la
palabra:
Aplicamos a cada número la función f(x)=x+4 para obtener
que retornado al alfabeto inglés, sustituyendo cada valor por su equivalente,
queda GIWEV .
Ahora, con la misma clave (1,4), buscamos descifrar FVYXYW . El valor
de cada letra es
Tomando f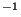 (x)=x-4, tenemos el resultado
que retornado al alfabeto inglés significa BRUTUS , texto plano
equivalente al cifrado FVYXYW .
(x)=x-4, tenemos el resultado
que retornado al alfabeto inglés significa BRUTUS , texto plano
equivalente al cifrado FVYXYW .
Si en el cifrado de un mensaje obtuvieramos que f(x) 25 (genéricamente, f(x)
25 (genéricamente, f(x) m-1), como trabajamos
con enteros de módulo m, deberíamos dividir f(x) por m, considerando
el resto entero como la cifra adecuada. Así, si f(x)=26, tomamos mod(26,26)=0
(el resto de la división entera), por lo que situaríamos una A en
el texto cifrado.
m-1), como trabajamos
con enteros de módulo m, deberíamos dividir f(x) por m, considerando
el resto entero como la cifra adecuada. Así, si f(x)=26, tomamos mod(26,26)=0
(el resto de la división entera), por lo que situaríamos una A en
el texto cifrado.
Es obvio que el cifrado Caesar tiene 26 claves diferentes (utilizando el alfabeto
inglés), incluyendo la clave de identidad (b=0), caso en el que el texto
cifrado y el texto en claro son idénticos. Así pues, no resultaría
muy difícil para un criptoanalista realizar un ataque exhaustivo, buscando
en el texto cifrado palabras en claro con significado en el lenguaje utilizado.
Por tanto, este criptosistema es claramente vulnerable para un atacante, no ofreciendo
una seguridad fiable en la transmisión de datos confidenciales.
El sistema de cifrado de Vigenère (en honor al criptógrafo francés
del mismo nombre) es un sistema polialfabético o de sustitución
múltiple. Este tipo de criptosistemas aparecieron para sustituir a los
monoalfabéticos o de sustitución simple, basados en el Caesar, que
presentaban ciertas debilidades frente al ataque de los criptoanalistas relativas
a la frecuencia de aparición de elementos del alfabeto. El principal elemento
de este sistema es la llamada Tabla de Vigenère, una matriz de caracteres
cuadrada, con dimensión 26x26, que se muestra en la tabla 14.1.
Tabla 14.1: Tableau Vigènere
| |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| A |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| B |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
| C |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
| D |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
| E |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
| F |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
| G |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
| H |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
| I |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
| J |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
| K |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
| L |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
| M |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
| N |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| O |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
| P |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
| Q |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
| R |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
| S |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
| T |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
| U |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
| V |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
| W |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
| X |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
| Y |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
| Z |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
|
La clave del sistema de cifrado de Vigenère es una palabra de k letras,
k 1 siempre, del alfabeto Z
1 siempre, del alfabeto Z utilizado anteriormente. Esta palabra es un elemento del producto
cartesiano Z
utilizado anteriormente. Esta palabra es un elemento del producto
cartesiano Z xZ
xZ x...xZ
x...xZ (k veces), que es justamente el alfabeto
del Criptosistema de Vigenère. De esta forma, el mensaje a cifrar en texto
claro ha de descomponerse en bloques de k elementos -letras- y aplicar sucesivamente
la clave empleada a cada uno de estos bloques, utilizando la tabla anteriormente
proporcionada.
(k veces), que es justamente el alfabeto
del Criptosistema de Vigenère. De esta forma, el mensaje a cifrar en texto
claro ha de descomponerse en bloques de k elementos -letras- y aplicar sucesivamente
la clave empleada a cada uno de estos bloques, utilizando la tabla anteriormente
proporcionada.
Veamos un sencillo ejemplo: Queremos codificar la frase La abrumadora soledad
del programador utilizando la clave prueba. En primer lugar, nos fijamos
en la longitud de la clave: es de seis caracteres. Así, descomponemos la
frase en bloques de longitud seis; aunque el último bloque es de longitud
tres, esto no afecta para nada al proceso de cifrado:
laabru madora soleda ddelpr ograma dor
Ahora, aplicamos a cada bloque la clave prueba y buscamos los resultados
como entradas de la tabla de Vigenère:
laabru madora soleda ddelpr ograma dor
prueba prueba prueba prueba prueba pru
arufsu brxhsa igfiea suyoqr exmena sgm
Por ejemplo, la primera a del texto cifrado corresponde a la entrada (l,p),
o, equivalentemente, (p,l) de la tabla de Vigenère. Finalmente, vemos que
el texto cifrado ha quedado arufsu brxhsa igfiea suyoqr exmena sgm .
Este método de cifrado polialfabético se consideraba invulnerable
hasta que en el S.XIX se consiguieron descifrar algunos mensajes codificados con
este sistema, mediante el estudio de la repetición de bloques de letras:
la distancia entre un bloque y su repetición suele ser múltiplo
de la palabra tomada como clave.
Una mejora sobre el cifrado de Vigenère fué introducida por el sistema
de Vernam, utilizando una clave aleatoria de longitud k igual a la del mensaje.
La confianza en este nuevo criptosistema hizo que se utilizase en las comunciaciones
confidenciales entre la Casa Blanca y el Kremlin, hasta, por lo menos, el año
1987.
El DEA ( Data Encryption Algorithm ) o DES ( Data Encryption Standard
) es desde 1977 de uso obligatorio en el cifrado de informaciones gubernamentales
no clasificadas (anunciado por el National Bureau of Standards , USA).
Este criptosistema fué desarrollado por IBM como una variación de
un criptosistema anterior, Lucifer, y posteriormente, tras algunas comprobaciones
llevadas a cabo por la NSA estadounidense, pasó a transformarse en el que
hoy conocemos como DES. Este criptosistema puede ser implementado tanto en software
como en chips con tecnología VLSI ( Very Large Scale Integration
), alcanzando en hardware una velocidad de hasta 50 Mbs. Un ejemplo de implantación
hard puede ser PC-Encryptor, de Eracom, y un ejemplo de implantación en
software es DES-LOCK, de la empresa Oceanics.
El DES es un sistema de clave privada tanto de cifrado como de descifrado. Posee
una clave de entrada con una longitud de 64 bits, produciendo una salida también
de 64 bits, con una clave de 56 bits (el octavo bit de cada byte es de paridad),
llamada clave externa, en la que reside toda la seguridad del criptosistema, ya
que el algoritmo es de dominio público. Cada trozo de 64 bits de los datos
se desordena según un esquema fijo a partir de una permutación inicial
conocida como IP. A continuación, se divide cada uno de los trozos en dos
mitades de 32 bits, que se someten a un algoritmo durante 16 iteraciones. Este
algoritmo básico que se repite 16 veces (llamadas vueltas), utiliza en
cada una de ellas 48 de los 56 bits de la clave (estos 48 bits se denominan clave
interna, difrerente en cada vuelta). Estas claves internas se utilizan en un orden
para cifrar texto (llamemoslas K , K
, K ,...,K
,...,K ) y en el orden inverso (K
) y en el orden inverso (K ,..., K
,..., K ) para descifrarlo. En
cada una de las vueltas se realizan permutaciones, sustituciones no lineales (que
constituyen en sí el núcleo del algoritmo DES) y operaciones lógicas
básicas, como la XOR. La mitad derecha se transfiere a la mitad izquierda
sin ningún cambio; también se expande de 32 hasta 48 bits, utilizando
para ello una simple duplicación. El resultado final de una iteración
es un XOR con la clave interna de la vuelta correspondiente. Esta salida se divide
en bloques de 6 bits, cada uno de los cuales se somete a una sustitución
en un bloque de 4 bits (bloque-S, con un rango 0...63) dando una salida también
de 4 bits (rango decimal 0...15) que a su vez se recombina con una permutación
en un registro con longitud 32 bits. Con el contenido de este registro se efectua
una operación XOR sobre la mitad izquierda de los datos originales, convirtiéndose
el nuevo resultado en una salida (parte derecha) de 32 bits. Transcurridas las
dieciseis vueltas, las dos mitades finales de 32 bits cada una se recombinan con
una permutación contraria a la realizada al principio (IP), y el resultado
es un criptograma de 64 bits.
) para descifrarlo. En
cada una de las vueltas se realizan permutaciones, sustituciones no lineales (que
constituyen en sí el núcleo del algoritmo DES) y operaciones lógicas
básicas, como la XOR. La mitad derecha se transfiere a la mitad izquierda
sin ningún cambio; también se expande de 32 hasta 48 bits, utilizando
para ello una simple duplicación. El resultado final de una iteración
es un XOR con la clave interna de la vuelta correspondiente. Esta salida se divide
en bloques de 6 bits, cada uno de los cuales se somete a una sustitución
en un bloque de 4 bits (bloque-S, con un rango 0...63) dando una salida también
de 4 bits (rango decimal 0...15) que a su vez se recombina con una permutación
en un registro con longitud 32 bits. Con el contenido de este registro se efectua
una operación XOR sobre la mitad izquierda de los datos originales, convirtiéndose
el nuevo resultado en una salida (parte derecha) de 32 bits. Transcurridas las
dieciseis vueltas, las dos mitades finales de 32 bits cada una se recombinan con
una permutación contraria a la realizada al principio (IP), y el resultado
es un criptograma de 64 bits.
Aunque no ha sido posible demostrar rigurosamente la debilidad del criptosistema
DES, y actualmente es el más utilizado en el mundo entero, parece claro
que con las actuales computadoras y su elevada potencia de cálculo, una
clave de 56 bits (en la que recordemos, reside toda la seguridad del DES) es fácilmente
vulnerable frente a un ataque exhaustivo en el que se prueben combinaciones de
esos 56 bits. Hay que resaltar que el tamaño inicial de la clave, en el
diseño de IBM, era de 128 bits; la razón de la disminución
no se ha hecho pública hasta el momento. Por si esto fuera poco, otro factor
que ha aumentado las controversias y discusiones acerca de la seguridad del DES
son dos propiedades del algoritmo: la propiedad de complementación, que
reduce el tiempo necesario para un ataque exhaustivo, y la propiedad de las claves
débiles, dada cuando el proceso de cifrado es idéntico al de descifrado
(K =K
=K , K
, K =K
=K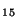 ,..., K
,..., K =K
=K ), que sucede con cuatro claves del criptosistema.
Otro secreto de IBM (a instancias de la NSA) es la elección y diseño
de las cajas que DES utiliza para el cifrado. No se puede evitar el pensar
que el gobierno estadounidense precise un criptosistema con la robustez necesaria
para que nadie, excepto ellos, pueda descifrarlo.
), que sucede con cuatro claves del criptosistema.
Otro secreto de IBM (a instancias de la NSA) es la elección y diseño
de las cajas que DES utiliza para el cifrado. No se puede evitar el pensar
que el gobierno estadounidense precise un criptosistema con la robustez necesaria
para que nadie, excepto ellos, pueda descifrarlo.
A la vista de estos hechos, la idea de que el DES no va a seguir siendo el algoritmo
de cifrado estándar en las instituciones estadounidenses se va generalizando
poco a poco. Por tanto, va a ser necesario sustituirlo por otro algoritmo más
robusto frente a los ataques. Siguiendo esta línea, Xuejia Lai y James
Massey, dos prestigiosos criptógrafos, desarrollaron, a finales de la década
de los ochenta, el algoritmo IDEA ( International Data Encryption Algorithm
), compatible con el DES (para aprovechar el gran número de equipos que
utilizan este algoritmo), y con una robustez garantizada por la clave de 128 bits
que utiliza este cifrador de bloques y las complejas operaciones utilizadas para
evitar el éxito de un posible atacante, que van desde técnicas de
difusión hasta adiciones módulo 2 .
.
El algoritmo IDEA está siendo ampliamente aceptado en diversas aplicaciones
informáticas orientadas a la seguridad de los datos; numerosos programas
destinados a trabajar en red utilizan ya este algoritmo como el principal de cifrado.
Este sistema de clave pública fué diseñado en 1977 por los
profesores del MIT ( Massachusetts Institute of Technology ) Ronald R.
Rivest, Adi Shamir y Leonard M. Adleman, de ahí las siglas con las que
es conocido. Desde entonces, este algoritmo de cifrado se ha convertido en el
prototipo de los de clave pública.
La seguridad de RSA radica en la dificultad de la factorización de números
grandes: es fácil saber si un número es primo, pero es extremadamente
difícil obtener la factorización en números primos de un
entero elevado, debido no a la dificultad de los algoritmos existentes, sino al
consumo de recursos físicos (memoria, necesidades hardware...incluso tiempo
de ejecución) de tales algoritmos. Se ha demostrado que si n es el número
de dígitos binarios de la entrada de cualquier algoritmo de factorización,
el coste del algoritmo es  (2n), con un tiempo de ejecución perteneciente
a la categoría de los llamados problemas intratables.
(2n), con un tiempo de ejecución perteneciente
a la categoría de los llamados problemas intratables.
Veamos el funcionamiento del algoritmo RSA: si un usuario A desea enviar información
cifrada, ha de elegir aleatoriamente dos números primos grandes (del orden
de cien dígitos), p y q. Estos números se han de mantener en secreto.
Si llamamos N (N se conoce como módulo) al producto p*q, el usuario ha
de determinar otro entero, d, llamado exponente privado, que cumpla
mcd(d,(p-1)*(q-1))=1, d

N
 (N), función de Euler, han de ser primos. Con estos datos,
ya tenemos la clave privada del cifrado: el par (N,d). Para obtener la clave pública,
hallamos el inverso multiplicativo del número d respecto de
(N), función de Euler, han de ser primos. Con estos datos,
ya tenemos la clave privada del cifrado: el par (N,d). Para obtener la clave pública,
hallamos el inverso multiplicativo del número d respecto de  (N), de la forma e*d=1 mod
(N), de la forma e*d=1 mod  (N). Calculado
este entero e, llamado exponente público, la clave pública será
el par (N,e).
(N). Calculado
este entero e, llamado exponente público, la clave pública será
el par (N,e).
Una vez el emisor A dispone de sus claves pública y privada, podría
enviar un mensaje cifrado, que llamaremos m, a un posible receptor, mediante la
operación
c=m

mod N
El receptor del criptograma, realizaría la siguiente operación de
descifrado:
m=c

mod N
El sistema RSA ha permanecido invulnerable hasta hoy, a pesar de los numerosos
ataques de criptoanalistas. Es teóricamente posible despejar d para obtener
la clave privada, a partir de la función de descifrado, resultando
d=log

m(mod(p-1))
 b(n), necesarias para descifrar
el mensaje, es algorítmicamente inviable sin ninguna información
adicional, debido al elevado tiempo de ejecución del algoritmo. Aunque
cuando los factores de p-1 son pequeños existe un algoritmo, desarrollado
por Pohlig y Hellman de orden O(log
b(n), necesarias para descifrar
el mensaje, es algorítmicamente inviable sin ninguna información
adicional, debido al elevado tiempo de ejecución del algoritmo. Aunque
cuando los factores de p-1 son pequeños existe un algoritmo, desarrollado
por Pohlig y Hellman de orden O(log p), éste es otro de los algoritmos catalogados como intratables,
vistos anteriormente.
Durante 1984 y 1985 ElGamal desarrolló un nuevo criptosistema de clave
pública basado en la intratabilidad computacional del problema del logaritmo
discreto: obtener el valor de x a partir de la expresión
p), éste es otro de los algoritmos catalogados como intratables,
vistos anteriormente.
Durante 1984 y 1985 ElGamal desarrolló un nuevo criptosistema de clave
pública basado en la intratabilidad computacional del problema del logaritmo
discreto: obtener el valor de x a partir de la expresión
y

a
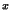
(mod p)
Aunque generalmente no se utiliza de forma directa, ya que la velocidad de cifrado
y autenticación es inferior al RSA, y además las firmas producidas
son más largas (<el doble de largo que el texto original!), el algoritmo
de ElGamal es de gran importancia en el desarrollo del DSS ( Digital Signature
Standard ), del NIST ( National Institute of Standards and Technology
).
En este sistema, para generar un par clave pública/privada, se escoge un
número primo grande, p, y dos enteros x y a, 1 x
x p-1, 1
p-1, 1 a
a p-1, y se calcula
p-1, y se calcula
y=a
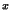
(mod p)
Para firmar un determinado mensaje, el emisor elige un entero aleatorio, k, 0 k
k p-1, no usado con anterioridad,
y con la restriccitricción que k sea relativamente primo a (p-1), y computa
p-1, no usado con anterioridad,
y con la restriccitricción que k sea relativamente primo a (p-1), y computa
r=a mod p
mod p
s=[k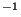 (m-xr)] mod (p-1),
(m-xr)] mod (p-1),
donde k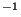 es el inverso de k mod (p-1); así,
es el inverso de k mod (p-1); así,
k* k
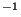
=1 mod (p-1).
 r
r mod p y comprobar si coincide
con a
mod p y comprobar si coincide
con a mod p:
El criptosistema de ElGamal tiene una característica determinante que lo
distingue del resto de sistemas de clave pública: en el cifrado se utiliza
aparte de la clave pública del receptor, la clave privada del emisor.
En 1978 McEliece presentó un nuevo criptosistema de clave pública,
basado en la Teoría de la Codificación algebraica. Dado que esta
teoría es muy compleja, los expertos recomiendan una familiarización
matemática preliminar con la Teoría de la Codificación, los
Códigos de Goppa, y los Cuerpos de Galois.
mod p:
El criptosistema de ElGamal tiene una característica determinante que lo
distingue del resto de sistemas de clave pública: en el cifrado se utiliza
aparte de la clave pública del receptor, la clave privada del emisor.
En 1978 McEliece presentó un nuevo criptosistema de clave pública,
basado en la Teoría de la Codificación algebraica. Dado que esta
teoría es muy compleja, los expertos recomiendan una familiarización
matemática preliminar con la Teoría de la Codificación, los
Códigos de Goppa, y los Cuerpos de Galois.
En el sistema de McEliece, cada usuario ha de elegir un polinomio irreducible
de grado t, y construir una matriz generadora del correspondiente código
de Goppa, matriz G, de orden kxn. También ha de calcular G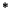 , matriz generadora de código
lineal tal que no exista un algoritmo computable que corrija los errores con éste
código en un tiempo pequeño, obtenida a partir de la expresión
, matriz generadora de código
lineal tal que no exista un algoritmo computable que corrija los errores con éste
código en un tiempo pequeño, obtenida a partir de la expresión
G
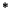
=S*G*P,
Supongamos que un emisor A quiere enviar un mensaje al receptor B. Para ello,
representará el mensaje como un conjunto de cadenas binarias, m, de longitud
k bits, y enviará
el mensaje cifrado de n bits
bits, y enviará
el mensaje cifrado de n bits
c=m*G

+e,
 y peso p
y peso p  que dificulta el criptoanálisis de
un potencial atacante, por razones en las que no vamos a entrar.
que dificulta el criptoanálisis de
un potencial atacante, por razones en las que no vamos a entrar.
Cuando B recibe el mensaje, ha de calcular
c*P
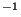
=m*S*G*P*P
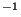
+e*P
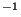
=(m*S)*G+e´
e´=e*P
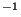
 .
.
Llamando m´=m*S, el receptor B puede calcular ahora el mensaje original,
a partir de
m=m´*S
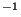
A lo largo de la historia han existido multitud de métodos para ocultar
información. Quizás los más conocidos hayan sido la tinta
invisible, muy utilizada durante la Segunda Guerra Mundial, o las marcas de cualquier
tipo sobre ciertos caracteres (desde pequeños pinchazos de alfiler hasta
trazos a lápiz que marcan un mensaje oculto en un texto), pero otros mecanismos
más 'extravagantes' también han sido utilizados: por ejemplo, afeitar
la cabeza de un mensajero y tatuar en el cuero cabelludo el mensaje, dejando después
que el crecimiento del pelo lo oculte; podemos repasar algunos modelos esteganográficos
cuanto menos curiosos en [Kah67].
Con el auge de la informática, el mecanismo esteganográfico más
extendido está basado en las imágenes digitales y su excelente capacidad
para ocultar información; aunque existen varias formas de conseguirlo ([vSTO94]),
la más básica consiste simplemente en sustituir el bit menos
significativo de cada byte por los bits del mensaje que queremos
ocultar; dado que casi todos los estándares gráficos tienen una
graduación de colores mayor de lo que el ojo humano puede apreciar, la
imagen no cambiará su apariencia de forma notable. Otros elementos donde
ocultar información son las señales de audio y el propio texto ([BGML96]), aunque no están tan extendidas como
la anterior.
Notas al pie
- ... ciencia15.1
- Hemos de dejar patente que la criptología es una ciencia,
aunque en muchos lugares aún se la considera un arte; por ejemplo,
en el Diccionario de la Real Academia de la Lengua Española.




Next: Algunas herramientas de
seguridad Up: Otros aspectos de la Previous: Otros aspectos de la Índice
General
mod p
(m-xr)] mod (p-1),