PILAS
PILA.(LIFO)(Last-In,First-Out:Ultimo en entrar,
primero en salir)
Es una
lista de elementos a la cual se puede insertar o eliminar elementos sólo por
uno de los extremos. En consecuencia, los elementos de una pila serán eliminados
en orden inverso al que se insertaron. Es decir, el último elemento que se mete
en la pila es el primero que se saca. Las pilas pertenecen al grupo de
datos lineales, ya que los componentes ocupan lugares sucesivos en la
estructura.
Existen numerosos casos prácticos en los que se
utiliza el concepto de pila.
Pila de latas en un
supermercado
Pila de platos
Ejemplos prácticos de Pilas.
**El cocinero cuando necesita un plato limpio, tomará el que está encima de
todos, que es el último que se colocó en la pila.
Representación de PILAS.
Las pilas no son estructuras fundamentales de datos,
es decir, no están definidas como tales en los lenguajes de programación (como
lo están por ejemplo los arreglos). Las pilas pueden representarse mediante el
uso de:
*Arreglos.
*Listas enlazadas.
PILA
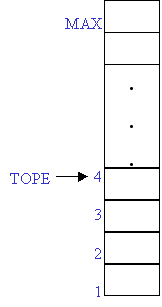
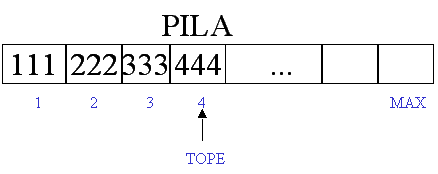
a) Pila
Llena
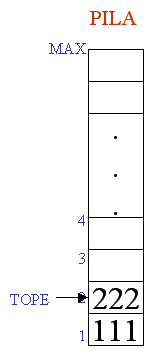
b) Pila con algunos
elementos
c) Pila vacía
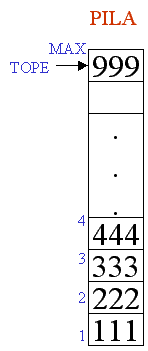
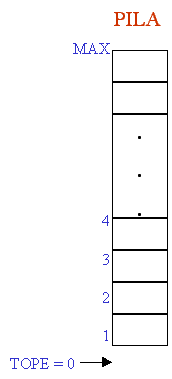
Donde TOPE = MAX, se quisiera insertar
otro elemento, se tendría un error de desbordamiento.
Una posible solución a este
tipo de errores consiste en definir pilas de gran tamaño, pero esto resultaría
ineficiente y costoso si sólo se utilizaran algunos elementos. No siempre es
posible saber con exactitud cuál es el número de elementos a tratar, por lo
tanto siempre existe la posibilidad de cometer un error de desbordamiento (si
se reserva menos espacio del que efectivamente se usará) o bien, de hacer uso
ineficiente de la memoria (si se reserva más espacio del que se empleará).
Doble PILA.
Existe una solución. Consiste en usar espacios compartidos de memoria para la
implementación de pilas. Supóngase que se necesitan dos pilas, cada una de
ellas con un tamaño máximo de N elementos. Se definirá un solo arreglo de 2*N
elementos, en lugar de dos arreglos de N elementos cada uno.
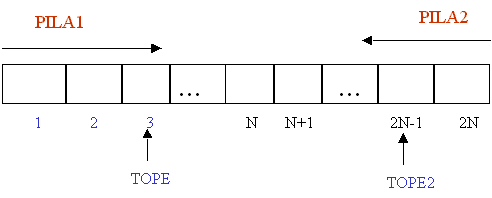
Representación de pilas en espacios compartidos.
** La pila1 ocupará de la posición 1 en adelante, mientras que la pila2
ocupará de la posición 2N hacia atrás (2N-1, 2N-2....) Si en algún punto del
proceso
** Otro error para pilas es que se trate de eliminar un elemento y la pila este
vacía. Este error se conoce con el nombre de subdesbordamiento.
OPERACIONES.
Las operaciones elementales que pueden realizarse son:
* Poner un elemento (Push)
* Quitar un elemento (Pop)
ALGORITMOS.
INSERTAR....
PONE(PILA,MAX,TOPE,DATO)
{ Este algoritmo pone el elemento DATO en PILA. Actualiza el valor de
TOPE. MAX es el máximo número de elementos que puede almacenar PILA}
Si TOPE < MAX entonces{Verifica que hay espacio
libre}
TOPE = TOPE +1
PILA[TOPE]=DATO
Si no Escribir "La pila esta
llena-Desbordamiento"
FinSi
ELIMINAR.
QUITA(PILA,MAX,TOPE,DATO)
{Este algoritmo saca el ultimo elemento de
Si TOPE > 0 entonces {Verifica que la pila no este vacía}
DATO=PILA[TOPE]
TOPE = TOPE -1
Si no Escribir "No hay elementos en
Fin Si
Ejemplo.
Inserción y Eliminación.
a)
b)
c)
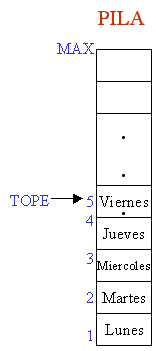
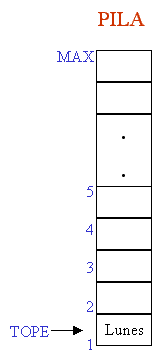
a) Si se pusieran los elementos lunes, martes, miércoles, jueves y
viernes (en este orden) en PILA.
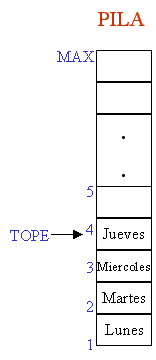
b) Si se quitara viernes el tope quedaría en jueves.
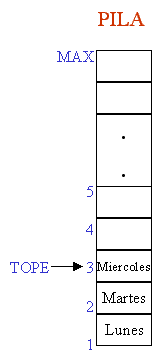
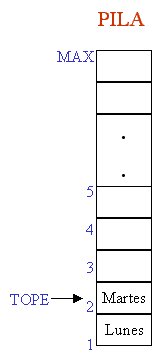
c) Si se pretendiera eliminar martes antes se tendría que quitar Jueves y Miércoles para que quede martes en la cima de la
pila y pueda extraerse.
APLICACIONES.
Las pilas son una estructura de datos muy usada en la
solución de diversos tipos de problemas. Algunos casos representativos son:
Llamada a Subprogramas.
Cuando se tiene un programa
que llama a subprograma, internamente se usan pilas para guardar el estado de
las variables del programa en el momento que se hace la llamada. Así, cuando
termina la ejecución del subprograma, los valores almacenados en la pila pueden
recuperarse para continuar con la ejecución del programa en el punto en cual
fue interrumpido. Además de las variables debe guardarse la dirección del
programa en la que se hizo la llamada, porque es a esa posición a la que
regresa el control del proceso.
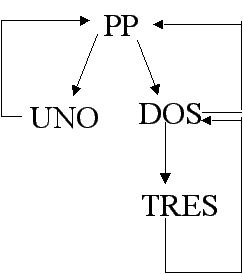
Por ejemplo, se tiene un programa
principal (PP) que llama a los subprogramas UNO y DOS. A su vez, el
subprograma DOS llama al subprograma TRES. Cada vez que la ejecución de
uno de los subprogramas concluye, se regresa el control al nivel inmediato
superior.
a) b) c) d) e) f)
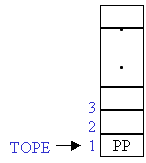

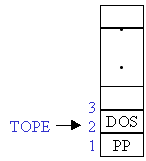

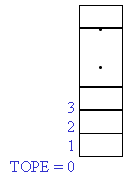
a) Cuando el programa PP llama a UNO, se guarda en una PILA la posición
en la que se hizo la llamada.
b) Al terminar UNO, el control se regresa a PP recuperando previamente la
dirección de
d) Cuando DOS llama a TRES, se pone en
e) Después de procesar TRES, se recupera la posición de DOS para continuar con
su ejecución.
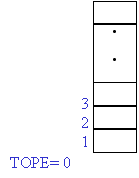
f) Al terminar DOS se regresa el control a PP obteniendo previamente la
dirección guardada en la pila.
Finalmente
podemos concluir que las pilas son necesarias en esta área de aplicaciones por
lo siguiente:
* Permiten guardar la dirección del programa (subprograma) desde donde se hizo
la llamada a otros subprogramas, para poder regresar y seguir ejecutándolo a
partir de la instrucción inmediata a la llamada.
* Permiten guardar el estado de las variables en el momento que se hace la
llamada, para poder seguir ocupándolas al regresar del subprograma.
Recursión.
Es un concepto amplio difícil
de precisar. Aparece en numerosas actividades de la vida diaria, por ejemplo,
en una fotografía de una fotografía. Otro caso de recursión
muy ilustrativo, es el que se presenta en los programas de televisión en los
cuales un periodista transfiere el control a otro periodista que se encuentra
en otra ciudad, y éste a su vez pudiera trasferirlo a un tercero. En este
capítulo nos limitaremos a tratar la recursión como
herramienta de programación.
La recursión
permite definir un objeto (problemas, estructuras de datos) en términos de sí
mismo. Casos típicos de estructuras de datos definidas de manera recursiva son
los árboles y las listas ligadas. Algunos ejemplos de problemas que se definen recursivamente se estudiarán posteriormente.
Un subprograma que se llama a
si mismo se dice que es recursivo. La recursión
en los subprogramas puede darse de dos maneras diferentes:
a)
b)

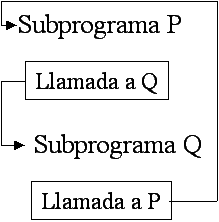
a) DIRECTA. El subprograma se
llama directamente a sí mismo.
Por ejemplo P es un subprograma y en alguna parte de él aparece una llamada a
sí mismo
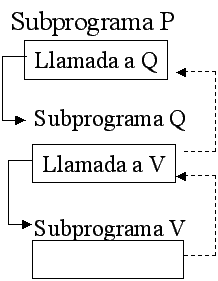
b) INDIRECTA. El subprograma llama a
otro subprograma, y éste a su vez llama al primero.
Por ejemplo:
*El subprograma P llama al subprograma Q y éste a su vez invoca al primero; es
decir el control regresa a P.
*El subprograma llama a otro y éste a un tercero. Una vez ejecutando el control regresa al subprograma que lo
llamó, lo mismo sucede en todos los niveles. Por ejemplo el subprograma P llama
al subprograma Q, y éste llama al subprograma V. Cuando V concluye, el control
regresa a Q y al terminar éste, el control se transfiere a
P.
Funcionamiento
interno de
Ejemplo:
Calcular Factorial de un número
N. N=4
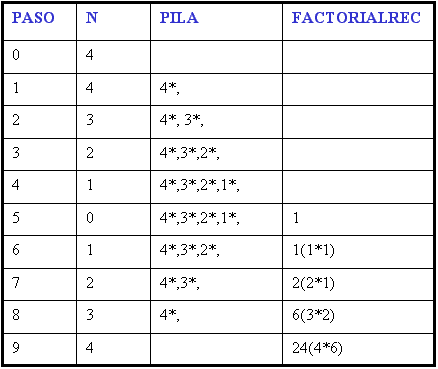
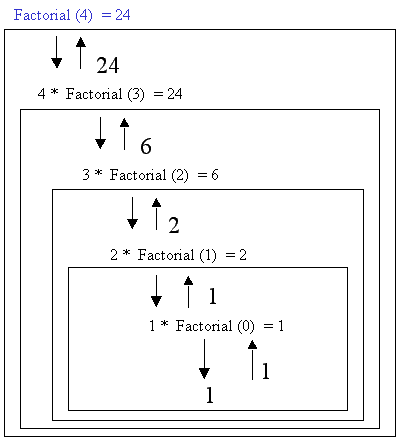
En
el primer paso N = 4; por lo tanto , siguiendo el algoritmo se debe hacerse 4 *
3!. Ante la imposibilidad de realizar esta
operación (porque primero debe calcularse 3!) se
guarda el valor de n en la pila y se continua trabajando con N = 3.
Con el nuevo valor de N procedemos
de manera similar que con N = 4. La diferencia radica en que la entrada, N,
esta mas cercana al estado básico. En consecuencia, en el paso 2 se agrega el
valor
El
problema de las Torres de Hanoi es un problema clásico de recursión,
ya que pertenece a la clase de problemas cuya solución se simplifica
notablemente al utilizar recursión.
Tratamiento de Expresiones
Aritméticas.
Un problema interesante en computación es poder
convertir expresiones en notación INFIJA a su equivalente en notación POSTFIJA(ó PREFIJA).
* Dada la expresión A+B se dice que está en notación INFIJA, y su nombre se
debe a que el operador (+) esta entre los operadores (A y B).
* Dada la expresión AB+ se dice que está en notación POSTFIJA, y su nombre se
debe a que el operador (+) esta después entre los operadores (A y B)
* Dada la expresión +AB se dice que está en notación PREFIJA, y su nombre se
debe a que el operador (+) esta antes de los operadores
(A y B).
La ventaja de usar expresiones en notación polaca
POSTFIJA ó PREFIJA radica en que no son necesarios los paréntesis para indicar
orden de operación, ya que este queda establecido por ubicación de los
operadores con respecto a los operandos.
Para convertir una expresión dada en notación INFIJA a
una notación POSTFIJA (ó PREFIJA), deberán establecerse previamente ciertas
condiciones:
-- Solamente se manejarán los siguientes operadores (Están dados ordenadamente
de mayor a menor según su prioridad de ejecución):
^ (potencia)
* / (multiplicación y
división)
+ - (suma y resta)
-- Los operadores de mas alta prioridad se ejecutan primero
-- Si hubiera en una expresión dos o mas operadores de igual prioridad,
entonces se procesarán de izquierda a derecha.
-- Las subexpresiones parentizadas
tendrán más prioridad que cualquier operador.
Ejemplo:
Se presenta 2 casos de traducción de notación INFIJA a
POSTFIJA. El primero de ellos es una expresión simple, mientras que el
segundo presenta un mayor grado de complejidad.
a) expresión infija
:X+Z*W
b)Expresión INFIJA:( X+Z )*W / T ^ Y - V

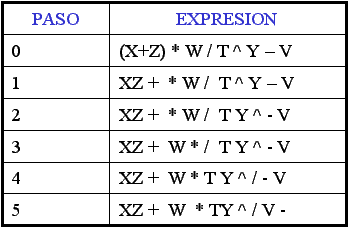
a)Expresión POSTFIJA:
XZW*+
b) Expresión POSTFIJA: XZ + W * T Y ^ / V -
A) El primer operador que se procesa durante la traducción de la expresión es
la multiplicación, Se coloca el operador de tal manera de que los operandos afectados por él lo precedan. Para el operador de
suma se sigue el mismo criterio, los dos operandos
los preceden. En este caso el primer operando es X y el segundo es ZW*
B) En el paso 1 se convierte la subexpresión parentizada por ser la de mas alta prioridad. Luego
se sigue con el operador de potencia, así con los demás según su jerarquía.
Como la multiplicación y la división tienen igual prioridad se procesa primero
la multiplicación por encontrarse más a la izquierda en la expresión. El
operador de la resta es el último que se mueve.
Algoritmo Conversión POSTFIJA.
CONV-POSTFIJA(EL,EPOS)
//Este algoritmo traduce una expresión infija EL a
postfija EPOS, haciendo uso de una pila PILA
//TOPE es una variable de tipo entero
TOPE = 0
Repetir mientras EL sea diferente de la cadena vacía.
Tomar el símbolo mas a la izquierda de EL, recortando luego la expresión.
Si símbolo es
paréntesis izquierdo entonces
{poner símbolo en PILA}
TOPE = TOPE +1
PILA [TOPE] = símbolo
Si no
Si símbolo es paréntesis Derecho entonces
Repetir mientras PILA [TOPE] <> paréntesis
Izquierdo
EPOS = PILA[TOPE]
TOPE = TOPE -1
fin -mientras
//Sacamos el paréntesis
izquierdo de PILA y no lo agregamos a EPOS.
TOPE = TOPE -1
Si no
Si símbolo es un operando entonces
agregar símbolo a EPOS
Si no {Es un operador}
Repetir mientras TOPE >0 y
prioridad del operador <= prioridad del operador de la
cima de la PILA
EPOS=EPOS + PILA[TOPE]
TOPE = TOPE - 1
Fin-mientras
TOPE =TOPE +1
PILA[TOPE]=Símbolo
fin si
finsi
finsi
fin-mientras
Repetir mientras TOPE > 0
EPOS=EPOS + PILA[TOPE]
TOPE = TOPE -1
Fin mientras
Escribir EPOS.
Algoritmo Conversión PREFIJA.
CONV-POSTFIJA(EL,EPOS)
//Este algoritmo traduce una expresión infija EL a
prefija EPRE, haciendo uso de una pila PILA
//TOPE es una variable de tipo entero
TOPE = 0
Repetir mientras EL sea diferente de la cadena vacía.
Tomar el símbolo mas a la derecha de EL, recortando luego la expresión.
Si símbolo es
paréntesis derecho entonces
{ poner
símbolo en PILA}
TOPE = TOPE +1
PILA [TOPE] = símbolo
Si no
Si símbolo es paréntesis izquierdo entonces
Repetir mientras PILA [TOPE] <> paréntesis
derecho
EPRE= EPRE+PILA[TOPE]
TOPE = TOPE -1
fin -mientras
//Sacamos el paréntesis
izquierdo de PILA y no lo agregamos a EPRE.
TOPE = TOPE -1
Si no
Si símbolo es un operando entonces
agregar símbolo a EPRE
Si no {Es un operador}
Repetir mientras TOPE >0 y
prioridad del operador < prioridad del operador de la
cima de la PILA
EPRE=EPRE + PILA[TOPE]
TOPE = TOPE - 1
Fin-mientras
TOPE =TOPE +1
PILA[TOPE]=Símbolo
fin si
finsi
finsi
fin-mientras
Repetir mientras TOPE > 0
EPRE=EPRE + PILA[TOPE]
TOPE = TOPE -1
Fin mientras
Escribir EPRE en forma invertida.
Ordenación
Generalmente el método de ordenación
rápida (QuickSort) por facilidad de implementación se
hace de manera recursiva. Sin embargo, para implementarlo de manera iterativa
(con ciclos) es necesario la utilización de 2 pilas auxiliares para ir almacenando
los limites inferiores y superiores de cada división o parte del
arreglo.